Télécharger le PDF de la revue

Télécharger le PDF de l'article

Mots-clés : Collégial - Pensée critique - Résolution de problèmes

 

 

Ed Hudson, Cégep John Abbott College

 

La réaction entre le cyanure d’hydrogène (HCN) gazeux et l’hydrogène gazeux forme de la méthylamine (CH₃NH₂) gazeuse. Le ∆H pour cette réaction est de -158 kJ/mol de méthylamine formée. Calculez l’énergie de liaison entre C et N dans HCN en utilisant les données suivantes...

Quelle est la masse de pétrole dans ce camion-citerne?

Laquelle de ces deux questions est la plus difficile sur le plan technique? À l’inverse, laquelle semble la plus intimidante ou la plus difficile pour une cégépienne ou un cégepien en Sciences de la nature, inscrit à un cours de chimie?

La première question (typique d’un examen de chimie générale au Collège John Abbott) repose sur des méthodes soigneusement enseignées et pratiquées, tandis que la seconde exige de l’initiative, de la rigueur dans l’utilisation des unités et la conviction que la réponse n’a pas besoin d’être parfaite pour être utile.

Dans notre société très complexe, technique et interdépendante, on considère que la numératie est essentielle à la participation démocratique et à la prise de décisions bien informées et fondées sur des données (Frankenstein, 2009; Sakurai et al., 2021). La pandémie de COVID-19 a mis cette nécessité d’autant plus en évidence.

De plus, pour prendre des décisions éclairées, il faut pouvoir appréhender des quantités bien plus grandes que celles de notre expérience quotidienne, et ces quantités sont difficiles à visualiser et à mettre en contexte. Quelle image mentale se fait-on, par exemple, de 730 millions de tonnes de CO2, soit les émissions annuelles du Canada en 2019 (Gouvernement du Canada, 2021)? Ou de 10 000 m³ par seconde, soit le débit typique du fleuve Saint-Laurent à Montréal (Gouvernement du Québec, 2022)?

Les étudiants et étudiantes en sciences de la nature devraient être bien placés pour développer leur numératie. La science a des racines mathématiques, et le programme de Sciences de la nature au cégep (tant le programme actuel que le nouveau) comprend trois à quatre cours de mathématique, ainsi que trois cours de physique et deux de chimie qui comportent des composantes mathématiques importantes. Or l’engagement des étudiants envers le contenu quantitatif est souvent mécanique, et n’exige ni ne soutient la réflexion critique sur les données quantitatives ou les estimations. Lorsque nous enseignons les compétences spécifiques, perdons-nous (ou nos étudiants et étudiantes perdent-ils) de vue les compétences générales?

Visualisations et estimations de Fermi : des outils pour développerla numératie

Cet article décrit mon expérience à intégrer des ateliers de visualisation et d’estimation de Fermi dans le cadre de deux cours au choix en Sciences de la nature au Collège John Abbott (202-DDN-05: Chimie de l’environnement et 202/203-ENV-AB: Le dilemme énergétique). Nommée d’après le célèbre physicien Enrico Fermi, qui aurait été un maitre dans ce type d’estimation, une estimation typique de Fermi consiste à faire une estimation raisonnable et éclairée d’une quantité inconnue, sur la base de données facilement estimables et de calculs simples qui peuvent idéalement être effectués dans sa tête.

Nous commençons un atelier typique par un « échauffement » au cours duquel nous estimons des quantités telles que la masse de notre édifice ou le nombre de mots dans la bibliothèque du cégep. Ensuite, les étudiants choisissent parmi une liste de questions créatives, suffisamment complexes et originales pour que les réponses ne puissent être trouvées par une recherche sur Internet. Ces questions peuvent être légèrement pratiques :

Pourriez-vous satisfaire la totalité des besoins annuels en eau de votre ménage en recueillant toute l’eau (sous forme de pluie ou de neige) qui tombe sur votre toit au cours d’une année? 

ou alors humoristiques :

Imagine que tu dois faire fonctionner ta cuisinière électrique uniquement avec l’électricité produite en pédalant sur un vélo stationnaire. Combien de temps devrais-tu pédaler par jour pour alimenter tes besoins en cuisine (ou ceux de ta famille)? Et, si ton chauffe-eau fonctionne de la même façon, combien de temps devrais-tu pédaler pour chauffer l’eau d’une douche?

Les écureuils sont assez communs à Sainte-Anne-de-Bellevue. La population entière de Sainte-Anne pourrait-elle subvenir à ses besoins en protéines en mangeant uniquement des écureuils « récoltés » dans la ville même?

Des équipes de deux ou trois étudiants et étudiantes disposent d’environ 20 minutes pour formuler une réponse plausible, ou du moins pour élaborer une stratégie pour la trouver. On leur rappelle quatre principes, qui peuvent facilement s’appliquer à d’autres cours ou contextes :

• Ne prenez pas un temps fou à chercher une donnée ou un nombre idéal sur le Web – vous faites de toute façon des approximations. Si vous ne pouvez pas trouver quelque chose rapidement, supposez une valeur raisonnable.
• Arrondissez et estimez. Deux chiffres significatifs sont suffisants.
• Faites très attention aux unités. Certaines sont facilement confondues et conduisent à des erreurs substantielles. (Une erreur fréquente est de confondre une quantité, par exemple, une énergie en kWh ou en joules, ou une masse de CO2, avec un flux, par exemple, une puissance en watts, ou le taux de CO₂ émis par an.).

et peut-être le plus important :

• Soyez audacieux. Essayez des choses. Ceci est sans risque.

Dans une estimation de Fermi classique, toutes les données d’entrée et tous les calculs doivent venir de la tête. Or j’autorise une certaine recherche sur Internet pour les données brutes en tant qu’entrée de la question, étant donné que ces données sont largement disponibles, mais que la compétence réside dans la façon de les utiliser de manière appropriée. Les équipes présentent ensuite à la classe leur réponse, leur stratégie et leurs hypothèses. Parfois, une discussion animée s’ensuit lorsque les étudiants et étudiantes remettent en question ou critiquent les hypothèses et les stratégies des autres.

Réactions des étudiants

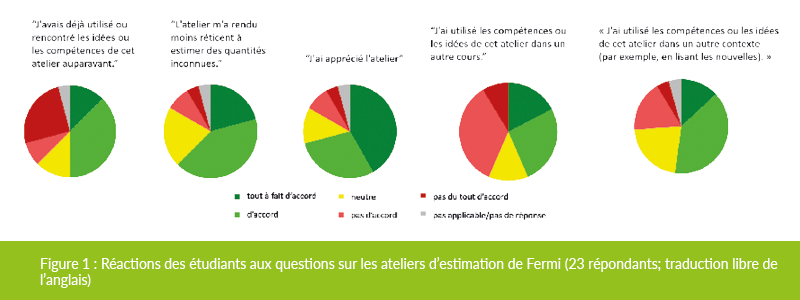
Les commentaires des étudiants indiquent qu’ils apprécient la valeur de ces idées (figure 1), malgré leur malaise initial à être poussés à les utiliser. Voici quelques commentaires écrits d’étudiants ayant participé à ces ateliers pendant un an [traduction libre] :

Cela vous fait adopter une nouvelle perspective lorsque vous abordez un problème, et cela aide à changer l’approche mentale de « brancher des chiffres » à « comprendre le problème ».

Cela nous a montré que nous n’avons pas besoin d’avoir peur d’une tâche qui est écrasante à première vue.

Voir comment les autres étudiants ont estimé différemment et ont parfois pris en compte des facteurs différents, mais les calculs avaient quand même un sens.

S’il vous plait, continuez à faire cet atelier. Il enseigne plus que de la chimie, c’est une compétence!

C’était l’un de mes ateliers préférés. J’aimerais que cette compétence (et la logique qui la sous-tend) soit davantage mise en avant dans l’enseignement général des sciences.

 

Conclusion

En exigeant de l’initiative, de la créativité et une utilisation critique des données, les problèmes de type Fermi peuvent contribuer à développer les compétences des étudiants et étudiantes en résolution de problèmes. Cependant, il est parfois difficile d’intégrer ces concepts dans nos cours de chimie obligatoires en raison de la quantité de contenu prescrit et du peu de temps disponible, ou peut-être plus en raison de la perception que le contenu est ce qui est le plus important (Peterson et al., 2020). Dans le cadre de la révision du programme de sciences en cours, il existe une opportunité d’encourager nos étudiants à développer une pensée critique et à penser comme des scientifiques (Cormier et Voisard, 2022). Mon souhait est qu’il y aura de la place dans ce programme pour développer une plus grande numératie en utilisant les outils décrits dans cet article.

 

Références

Cormier, C. et Voisard, B. (2022). Nouveau programme collégial québécois de Sciences de la nature: commentaire sur l’article de Désautels (2020) et pistes pour l’intervention. Can. J. Sci. Math. Techn. Educ., 22, 237-249. https://doi.org/10.1007/s42330-022-00192-8

Frankenstein, M. (2009). Developing a critical mathematical numeracy through real real-life word problems. Dans L. Verschaffel, B. Greer, W. Van Doorenet S. Mukhopadhyay (eds.), Words and Worlds (vol. 16, p. 111-130). Brill. https://doi.org/10.1163/9789087909383_008

Gouvernement du Canada. (2021). Émissions de gaz à effet de serre. https://www.canada.ca/fr/environnement-changement-climatique/services/indicateurs-environnementaux/emissions-gaz-effet-serre.html

Gouvernement du Québec. (2022). Suivi hydrologique de différentes stations hydrométriques. https://www.cehq.gouv.qc.ca/suivihydro/graphique.asp?NoStation=001003

Petersen, C. I., Baepler, P., Beitz, A., Ching, P., Gorman, K. S., Neudauer, C. L., Rozaitis, W., Walker, J.D. et Wingert, D. (2020). The tyranny of content: “Content Coverage” as a barrier to evidence-based teaching approaches and ways to overcome it. CBE- Life Sciences Education, 19(2). https://doi.org/10.1187/ cbe.19-04-0079

Sakurai, J., Sawatzki, C. et Tout, D. (2021, septembre). Real life numeracy contexts – the spark to ignite mathematics learning.Teacher.
https://www.teachermagazine.com/au_en/articles/real-life-numeracy-contexts-the-spark-to-ignite-mathematics-learning

Suggestions de lecture

Mahajan, S. (2010). Street-fighting mathematics: The art of educated guessing and opportunistic problem solving. MIT Press.

---

Spectre | Volume 52, numéro 1 | Novembre 2022

---

 

< RETOUR AU SOMMAIRE >

ARTICLE SUIVANT >